• Telefon : +40 728 88 22 88
  • Program de lucru : Vezi orarul!
  • Adresă : Bacău, str. Mihai Eminescu, nr. 1, bloc. A1
  • Home
  •  - 
  • Stiri
  •  - 
  • Test de evaluare grupele B

Test de evaluare grupele B

În prima săptămână cei de la grupele B au primit următorul test inițial. Le recomand și celor din celelalte grupe să încerce să-l rezolve.

PROGRAMARE CU RĂBDARE

Test grupa B – Proiecte

Trebuie să rezolvați cel puțin câte o problemă din fiecare categorie.

Categoria 1:

  1. Anii bisecți sunt divizibili cu patru, dar nedivizibili cu 100, cu excepția anilor divizibili prin 400. Astfel, anii 1900 și 2019 nu sunt bisecți, dar anii 2000 și 2016 sunt bisecți.Care dintre următoarele expresii C/C++ testează dacă valoarea variabilei n desemnează un an bisect?
    • (n%400<1)||(n%4==0)&&(n%100!=0)
    • (n%100!=0)&&(n%400==0)||(n%4==0)
    • (n%100!=0)&&(n%4==0)
    • (n%4==0)&&(n%100!=0)&&(n%400==0)
  1. Variabilele u, v, z, t memorează valori întregi astfel încât u < v și z < t. Precizează care dintre expresiile C/C++ de mai jos, atunci când este adevărată, implică faptul că intersecția intervalelor [u, v) și (z, t] este nevidă.
    • (u > t) && (v > z)
    • !((u > t) || (v > z))
    • (u <= t) && (v == z)
    • !((u > t) || (t > u))

Categoria 2:

  1. Fie x o variabilă întreagă care conține cel mai mic număr natural nenul, multiplu de 36, divizibil cu toate numerele prime mai mici decât 10. Precizați care dintre expresiile C/C++ de mai jos este adevărată.
    • (x<1000) && (x % 27 == 0)
    •  (x>1000) && ((x*x*x) % 1000 == 0)
    • ((x*x) / 16) % 2 == 0
    • (x % 100 == 0) || (x / 100 == 0)
  1. Pentru a reprezenta în limbajul C/C++ relațiile de prietenie dintr-un grup de oameni se folosesc următoarele definiții de date:
struct gr {
    int nrPers;
    int priet[50][50]; 
} om;

cu semnificația că în câmpul nrPers stocăm numărul de persoane din grup, iar priet[i][j] poate avea valoarea 1 (semnificând că omul cu numărul i este prieten cu omul cu numărul j), respectiv 0 (în caz contrar). Relația de prietenie se consideră reciprocă.

Cerințe:

a) Care din următoarele secvențe de atribuiri descrie în C/C++ faptul că oamenii cu numerele de ordine 3 și 5 devin prieteni.

a) om.priet[3][5]=1;
om.priet[5][3]=1;
 
b) gr.priet[3][5]=1;
gr.priet[5][3]=1;
 
c) priet.om[3][5]=1;
priet.om[5][3]=1;
 
d) priet.gr[3][5]=1;
priet.gr[5][3]=1;

b) Scrieți o secvență de cod C/C++ prin care puteți atribui variabilei întregi numarMaxim numărul maxim de relații de prietenie care pot exista în grupul definit mai sus.

Categoria 3:

  1. O tablă albă are p simboluri “A” și m simboluri “B” scrise pe ea. Poți alege oricare două simboluri pentru a le șterge și înlocui cu altul, în conformitate cu următoarele reguli
  • AA ⇒ B
  • AB sau BA ⇒ A
  • BB ⇒ B

Dacă vei continua să aplici aceste reguli de înlocuire cât mai mult timp posibil, ce valori ar trebui să aibă p și m ca la final să rămână un singur “A”?

  1. Un robot este poziționat în locul marcat cu o săgeată în harta de mai jos, având orientarea către susul paginii. Robotul poate să interpreteze următoarele comenzi:

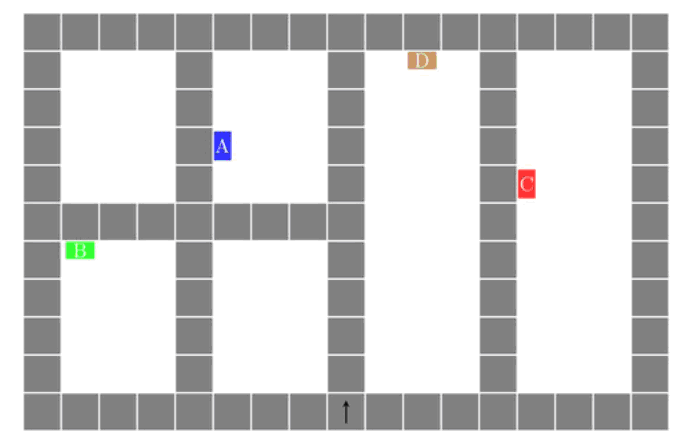
nI = mergi n pătrățele înainte

S/D = rotește-te cu 90 de grade la stânga/dreapta

n(commenzi) = execută comenzile dintre paranteze de n ori

O secvență de comenzi care va deplasa robotul din locația săgeții cu în fața stației C este:

  • 2I + 2(8I + D) + D + 2(4I + S)
  • 6I + 2(4I + S) + 5I + D + 3I + S
  • 6I + 2(4I + S) + 5I + 2(D) + 2I + D
  • 2I + 2(8I + D) + D + 2I + 4I + S

 Categoria 4:

  1. Considerăm un alfabet A format dintr-o mulțime finită de caractere. Un cuvânt este o secvență nevidă de caractere distincte din A. Lungimea unui cuvânt este numărul de caractere din care acesta este format. Un p-sistem (p ≥ 1) este definit ca o mulțime S de cuvinte, toate de lungime p, având proprietățile:

(P1) oricare două cuvinte din S au exact un caracter comun

și

(P2) orice caracter din alfabetul A apare în cel puțin un cuvânt din S.

Exemplu: Pentru A = {’a’, ’b’, ’c’}, mulțimea S = {”ab”, ”ac”} este un 2-sistem.

Scrie un 3-sistem peste alfabetul A = {’a’, ’b’, ’c’, ’d’, ’e’, ’f’}.

  1. O matrice cu 8 linii, formată doar din 0 și 1, are următoarele trei proprietăți:

(i) prima linie conține un singur element cu valoarea 1,

(ii) linia j conține de două ori mai multe elemente nenule decât linia j −1, pentru orice
j ∈{2,3, . . . , 8},

(iii) ultima linie conține un singur element cu valoarea 0.

Care este numărul total de elemente cu valoarea 0 din matrice?

  1. 777
  2. 769
  3. 528
  4. nu există o astfel de matrice.

Categoria 5:

  1. O rețea de comparatori de tip n (n ≥ 2) și de dimensiune m (m ≥ 1) este o secvență (c1, c2, . . . , cm) în care fiecare element cm, numit comparator, este o pereche de numere întregi (j, k) cu proprietatea 1 ≤ j < k ≤ n.

Exemplu: Rețeaua R = ((1, 2),(2, 3)) are tipul 3 și dimensiunea 2.

Daca a este un vector de n numere întregi și R este o rețea, notăm cu R(a) vectorul obținut aplicând următoarele transformări lui a:

pentru fiecare comparator ci = (j, k), 1 ≤ i ≤ m din R, în ordinea în care aceștia apar în rețea, dacă a[j] > a[k] atunci în vectorul a interschimbăm valorile de la pozițiile j și k.

Exemplu: Pentru R = ((1, 2),(2, 3)) și a = (30, 20, 10) avem R(a) = (20, 10, 30).

Cerințe:

a) Fie R = ((2, 4),(1, 2),(3, 4),(2, 3)) și a = (40, 30, 20, 10). Calculați R(a) și scrieți valorile intermediare ale vectorului a corespunzătoare transformărilor efectuate.

b) Dați exemplu de o rețea R de tip 4 cu proprietatea că pentru orice vector a format din 4 numere întregi distincte, R(a) va avea elementele ordonate crescător. Justificare.

  1. Se consideră algoritmul de mai jos. S-a notat cu x%y restul împărţirii numărului întreg x la numărul întreg nenul y şi cu [a] partea întreagă a numărului real a.
  2. a) Scrieți ce se va afișa dacă se citește 18?
  3. b) Dați exemplu de un număr natural n<100, astfel încât algoritmul să afișeze 6.
  4. c) Scrieți algoritmul sub forma unei funcții recursive echivalente (în pseudocod sau în C/C++)
citește n
p¬0
┌cât timp n>0 execută
│   ┌dacă n%3 = 0 atunci
│   │     n¬ [n/3]
│   │altfel
│   │    ┌dacă n%2 = 1 atunci
│   │    │     n¬ [n/2]
│   │    │altfel
│   │    │     n¬n-1
│   │    └■
│   └■
│    p¬p+1
└■
scrie p

 

27 Comments

  • comision tarjeta de credito binance

    - 04/04/2023 at 03:16

    Your article helped me a lot, is there any more related content? Thanks!

  • blog comment policy example

    - 20/04/2023 at 06:51

    vtvqsaseu paoeo ksumulh xtup sdmlmqvcsbrkipi

  • Dark web market links 2023

  • แทงบอลออนไลน์

  • gate io

    - 04/05/2023 at 06:38

    I am an investor of gate io, I have consulted a lot of information, I hope to upgrade my investment strategy with a new model. Your article creation ideas have given me a lot of inspiration, but I still have some doubts. I wonder if you can help me? Thanks.

  • Mxngmb

    - 07/05/2023 at 19:50

    cialis pills 20mg tadalafil 20mg usa buy ed pills best price

  • 註冊binance

    - 15/05/2023 at 19:24

    Thank you for your sharing. I am worried that I lack creative ideas. It is your article that makes me full of hope. Thank you. But, I have a question, can you help me?

  • gateio

    - 27/05/2023 at 01:50

    I may need your help. I’ve been doing research on gate io recently, and I’ve tried a lot of different things. Later, I read your article, and I think your way of writing has given me some innovative ideas, thank you very much.

  • สล็อตpg

  • gateio

    - 05/06/2023 at 04:26

    The point of view of your article has taught me a lot, and I already know how to improve the paper on gate.oi, thank you. https://www.gate.io/pt/signup/XwNAU

  • Inversores institucionales en gate.io

    - 18/06/2023 at 02:05

    Reading your article has greatly helped me, and I agree with you. But I still have some questions. Can you help me? I will pay attention to your answer. thank you.

  • Erickduh

    - 18/06/2023 at 03:54

    https://whyride.info/ – whyride

  • Buat Akun di Binance

    - 03/07/2023 at 07:16

    I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article. https://accounts.binance.com/id/register?ref=V2H9AFPY

  • Erickduh

    - 05/07/2023 at 13:31

    whyride

  • Ved

    - 19/07/2023 at 22:14

    Strip Poker może być również grany online. Dostawcy Strip Poker online (tacy jak Racy Rivals) zdecydowanie celują w heteroseksualnych mężczyzn. Różnica w stosunku do zwykłego pokera polega na tym, że widzisz również (nagrane) wideo kobiety. Grasz przeciwko komputerowym przeciwnikom. Za każdym razem, gdy komputer przegrywa, kobieta na wideo zdejmuje z niego część ubrania. Jeśli przegrasz, możesz wybrać, czy chcesz się rozebrać, czy nie. W końcu nikt cię nie widzi. Moim zdaniem prawdziwy Strip Poker jest zdecydowanie bardziej zabawny. Ale jest to dobra alternatywa, by ćwiczyć. Słowo „wymiękasz” nie kojarzy się dobrze w środowisku gimnazjalistów. Ci, którzy nie mają w sobie odwagi, najczęściej kończą stojąc samotnie na każdej przerwie pod klasą. Jedną z najnowszych gier gimnazjaliści nazwali właśnie tym zwrotem: „wymiękasz”. Zasady gry są bardzo proste. Dziewczyna lub chłopak losują dla siebie osobę do pary, która staje w bieliźnie naprzeciwko. Zabawa polega na dotykaniu poszczególnych części ciała.
    http://mk365.ipdisk.co.kr:8088/apps/gnuboard54/bbs/board.php?bo_table=free&wr_id=15071
    wroclawwroclovekasynocasinospielbank Gmina Wrocław chce we wrześniu ogłosić przetarg na teren przy stadionie Tarczyński Arena. Na działce o powierzchni ponad 5 ha ma powstać hala widowisk … Wysokim standardem może pochwalić się kasyno w kompleksie OVO w hotelu Hilton przy Podwalu. To najnowszy lokal hazardowy we Wrocławiu, zarządzany przez sieć Casinos Poland. Jest to największa inwestycja we Wrocławiu i jednocześnie wizytówka miasta. Z tego kasyna można nie wychodzić. W końcu niczego tu nie brakuje. Kasyna w Sopotu Czy Casinos Poland CP Sp. z o.o. Kasyno w Hotelu Marriott organizuje staże dla studentów? Casinos Poland Wrocław ulokowane jest na tyłach wielkiego Parku Juliusza Słowackiego. Tuż obok krzyżują się duże ulice Podwale oraz Słowackiego. Jeśli zdecydujecie się na spacer od strony Runku, dojście do obiektu zajmie wam nie więcej niż 10 minut. Polecamy udać się tam pieszo, ponieważ na miejscu mogą być problemy z parkowaniem – duży kompleks biurowo-usługowy OVO, w którym mieści się kasyno naziemne, codziennie odwiedzają tysiące osób.

  • Dave T Bolno NKSFB

  • JimmyGlymn

    - 07/08/2023 at 14:47

    prednisone 2 5 mg: http://prednisone1st.store/# prednisone acetate

  • Derektwime

    - 07/08/2023 at 20:42

    free online adult dating site: indian dating – dating sites into trampling

  • slot online

  • slot server thailand

  • Abina

    - 05/09/2023 at 20:49

    A member of the Genesys Club group of casinos, The Mandarin Palace are now owned by the same group that owns the GrandPrive group. The player complained he did not break any bonus rule. However, the casino’s opinion was different. The casino said every no deposit bonus could be used just once per IP address. Somehow the casino offered the same bonus for different casinos, the casino said the player used 3 times the bonus for one IP address. The player said it was always for a different casino. It was hard to decide as there was no evidence and no such things in the terms. The player complained he did not break any bonus rule. However, the casino’s opinion was different. The casino said every no deposit bonus could be used just once per IP address. Somehow the casino offered the same bonus for different casinos, the casino said the player used 3 times the bonus for one IP address. The player said it was always for a different casino. It was hard to decide as there was no evidence and no such things in the terms.
    http://pjh3.dothome.co.kr/bbs/board.php?bo_table=free&wr_id=16516
    Finally, there is Sloto’Cash Mobile, the ultimate in Vegas online slots casino gaming freedom. Our real money slot apps delivery is compatible with all mobile phones and tablets, the Sloto’Cash Mobile Casino travels comfortably in your pocket. Wherever you go, your Slotocash Casino slot machines are ready for real online casinos gaming action. Play slots online, real money slots, any time and any place. And the number of games. A Las Vegas casino, no matter how huge it appears, has a finite number of square feet, which means room for a finite number of games. Slotocash Casino resides in cyberspace, which is infinite. Every month we add more games, and there is literally no limit to our capacity to expand. Come see our enormous free slots and games selection, our match bonus picks, our online slots payout, best casinos table games and progressive jackpots, huge jackpots with highest payout percentages – you will be amazed.

  • pool villas in phuket

  • car detailing

  • Mok

    - 16/09/2023 at 11:03

    After the Bitcoin blockchain had operated for a number of years, successfully storing every Bitcoin transaction and surviving numerous attacks from hackers, many programmers and entrepreneurs wondered if its design could be replicated to create other kinds of secure ledgers unrelated to Bitcoin. Because blockchain technology is the technology behind the blockchain, it cannot be owned. It’s like the internet. But anyone can use the technology to run and own their own blockchains. A study published by Tata Communications in 2018 showed that 44% of organizations in its survey are adopting blockchain, but also alludes to the universal problems that arise from deploying new technologies. From an architectural level, the unsolved problem of scalability is emerging as a bottleneck to blockchain adoption and practical applications.
    https://jaidenbaxv528547.bloggip.com/20879173/manual-article-review-is-required-for-this-article
    Gain trust and grow your business with customer reviews. Second most liked instagram hashtags used with bitcoincharts Get The Ultimate Guide to Bitcoin™ now with the O’Reilly learning platform. For more information on customizing the embed code, read Embedding Snippets. Daily visitors: Copyright © 2023 testednet The first and most common type of Bitcoin chart tracks the Bitcoin exchange rate on an ongoing basis. The easiest way to do this is via a simple line chart, in which pricing for a given period (month, week, day, or hour) is plotted on the chart’s Y (vertical) axis, against the time period itself on the X (horizontal) axis. These individual price points are then connected via a … There is a blockchain with index through block 170,000 here:

  • YoungSofie Cam Model

    - 18/09/2023 at 14:11

    Everyone must take caution before sending personal information over the Internet and through meet new people on live chat.

  • Skrota bil Göteborg

  • slot online gacor

Leave a Reply